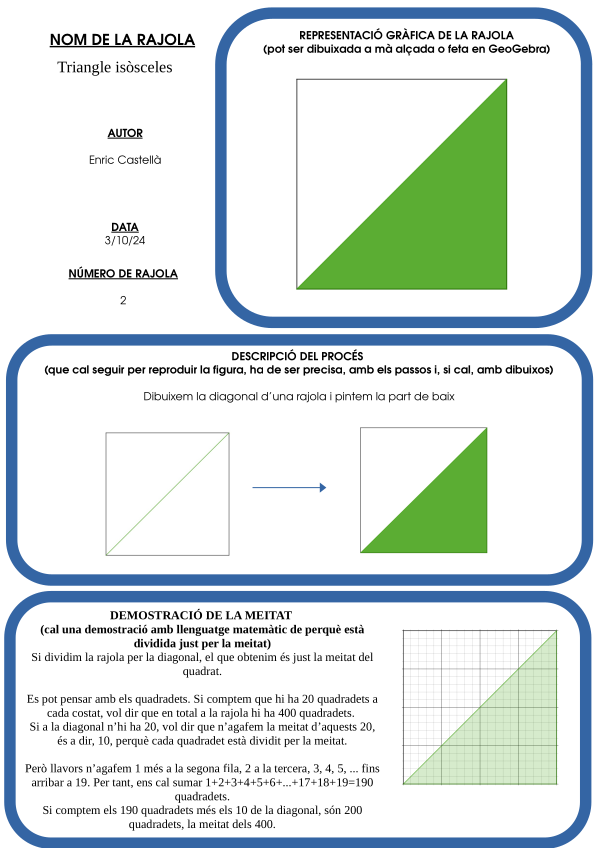
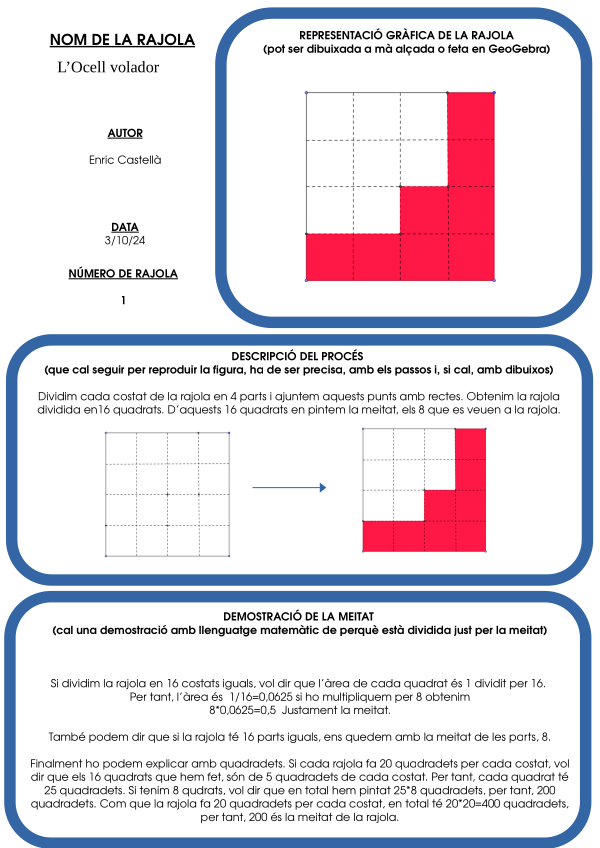
La meitat d'un quadrat

Donat un quadrat, una manera d'obtenir, dins d'ell, un polígon d'àrea la meitat, consisteix en:

Prendre els punts mitjos de dos costats oposats i unir-los amb un segment. D'aquesta manera obtenim un rectangle com el de la imatge:

Cliquem sobre la imatge de la rajola i obtenim una presentació del projecte Enrajolem! on es veuen dues maneres diferents de dividir la rajola per la meitat, però llavors ho extenem a ajuntar diverses rajoles i observem que hi ha moltes possibilitats diferents de mosaics. No t'oblidis de clicar a l'enllaç d'Enrajolat aleatori a la diapositiva d'Snap!

Repartim fulls quadriculats a tot l'alumnat, i demanem que construeixin diferents rajoles quadrades de 20x20 quadradets, de manera que obtinguin la meitat pintada.

Cal que comparteixin idees amb la resta de companys, tant els encerts com els errors dels diferents enfocaments i propostes que vagin veient. És molt important tenir en compte al sentit socioemocional en aquest projecte, es pot aprofitar molt bé per portar a terme una de les frases de l'Anton Aubanell "Tothom ha de tenir un moment de glòria a l'aula de matemàtiques" gràcies a que és una activitat de llindar baix (tothom pot començar a dividir per la meitat una rajola per més dificultats que tingui), és de sostre alt (perquè es pot estirar tant com vulguis a nivell matemàtic la creació, descripció i demostració matemàtica) i, finalment, és de parets amples (perquè es pot fer tant a mà com de forma digital). 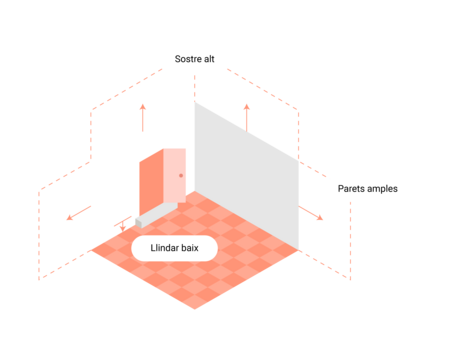En aquest sentit cal desmentir creences al respecte de les matemàtiques, com per exemple no deixant que ningú digui "que no serveix per les matemàtiques" i insistir en com l'error és el motor de l'aprenentatge. Podeu escoltar amb més profunditat la conferència inaugural de la XIX Jornada d'Ensenyament de les Matemàtiques d'Antoni Vila amb el títol "Trenquem mites: equivocar-se per aprendre" 

Ara, anem a centrar-nos en una sola rajola. Per cada rajola cal saber 4 dades:

(1) Cal donar un nom a la figura obtinguda. Es poden buscar referències, però cal ser precís i imaginatiu.

(2) Cal tenir el dibuix retallat del full quadriculat dins de la plantilla o la representació amb GeoGebra.

(3) Cal descriure el procés que cal seguir per reproduir la figura. Aquest relat ha de complir certes normes de concreció i, sobretot, una correcta utilització de la terminologia matemàtica.

(4) Demostrar que realment la solució és la meitat del quadrat. Aquesta demostració ha d'estar al nivell de l'alumnat i ha de ser a partir d'idees sorgides pròpies. Com més varietat d'idees, molt millor.

Repartim una Plantilla de rajola impresa per cada alumne i cal que omplin la seva primera rajola. És molt important que comencin escrivint amb llapis el que fan, per poder anar millorant a mesura que van venint a mostrar-nos el que van fent i nosaltres els hi anem dient com millorar-ho (llenguatge matemàtic, descripció del procés, demostració de que és la meitat, ...).

Podeu mirar aquest primer model de plantilla per observar un primer exemple les descripcions i argumentacions de cada apartat de la plantilla de rajola.

Durant el procés de creació de les rajoles, l'alumnat anirà aprenent a fer demostracions i explicacions de com descriure el procés a partir de les indicacions i suggeriments que els hi anirem donant com a feedback. En aquest punt és important compartir amb tota l'aula paraules, descripcions, processos interessants que s'han anat creant, per donar importància a la individualitat i donar importància amb el compartir per construir coneixement de forma col·lectiva.

És molt interessant donar bastides, indicacions o suggeriments de com s'hauria d'anar fent perquè l'alumnat vagi adoptant nou vocabulari i maneres d'expressar diferents idees. Una eina per mostrar el que volem dir és aquest vídeo, tant divertit com molt instructiu, on sorgeixen de manera natural dos grans idees: cal anar fent versions d'un procés per millorar-lo (com la papallona d'Austin) i cal ser molt precís quan donem instruccions perquè l'altra persona entengui el que li volem dir.

Continuem generant rajoles. En aquesta sessió podem mostrar aquest segon model de plantilla per poder fer les descripcions de les rajoles. I anar generant noves rajoles i, sobretot, anar donant feedback a l'alumnat perquè vagin aprenent i millorant les seves rajoles. Si es considera que ja en tenen una d'acabada, la poden escriure en bolígraf i pintar en colors la rajola.

Per poder mostrar el procés de millora, que s'entengui que quan venen a mostrar els seus escrits i les seves rajoles, és molt necessari rebre suggeriments per millorar-les, tant del professorat com del mateix alumnat. És per entendre això que passem el següent vídeo de la Papallona d'Austin:

Després de mostrar el vídeo de la papallona on incidirem en que l'error és part del procés de l'aprenentatge, que no és un punt de parada ni un punt de retrocés, si no que és un punt de reflexió per millorar cap endavant, els hi mostrem una segona plantilla construïda per donar exemples perquè millorin les seves rajoles:

Quan hem pogut recollir bastantes rajoles, no pas de tothom perquè sempre hi haurà dificultats en algun alumnat a la hora de poder acabar per complet una descripció de la rajola i, en canvi, d'una sola persona podem recollir diverses rajoles, és un bon moment per utilitzar una de les bastides d'en Jordi Domènech per promocionar la creativitat. La podeu trobar en el seu llibre "Aprenentatge basat en projectes per a STEAM. Breu manual pràctic", en concret fem servir la plantilla Cre3: Disrupcions per a la creativitat de l'itinerari Minerva. Es reparteix una copia impresa a tot l'alumnat i a través de la dinàmica 1-2-4, demanem que en silenci treballin la copia, pensant en diferents maneres de canviar i fer noves rajoles. Després en parelles comenten les reflexions i possibles millores que poden fer amb les seves rajoles per, finalment, fer-ho en grups de 4 persones.